モナドを理解せずともモナド教を信ずることは出来ますが,理解していればより深く納得できるでしょう.
操作 :: 型 -> 型 は,"型"から"型"へ写す"操作"の存在を表します.
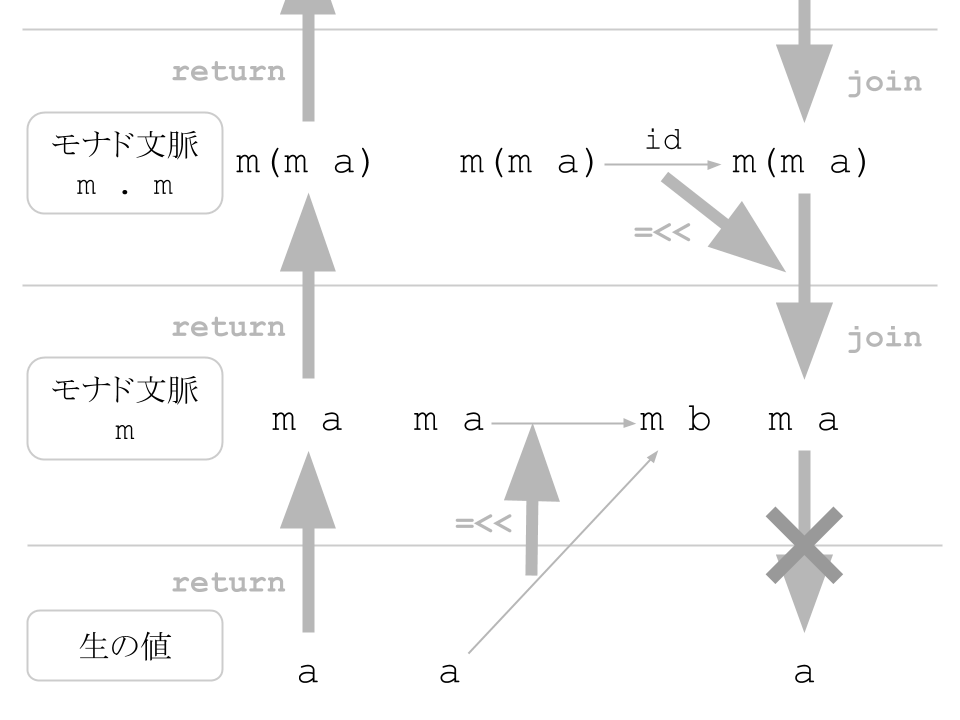
m が必要とする2つの操作:
return :: a -> m a で,値を保ちつつ文脈 m の中に入れ込むことが出来ます.
(=<<) :: (a -> m b) -> (m a -> m b) で,「値を文脈に入った別の値へ写す操作」を「文脈に入った値を同じ文脈に入った別の値へ写す操作」に変換します.
id :: a -> a は値をそのまま返す操作です.
id を =<< で変換して得られる操作 join :: m (m a) -> m a で,二重に文脈に入った値を一重の文脈に入った値に戻すことが出来ます.
m a -> a を持つ操作は,一般に用意されていません.
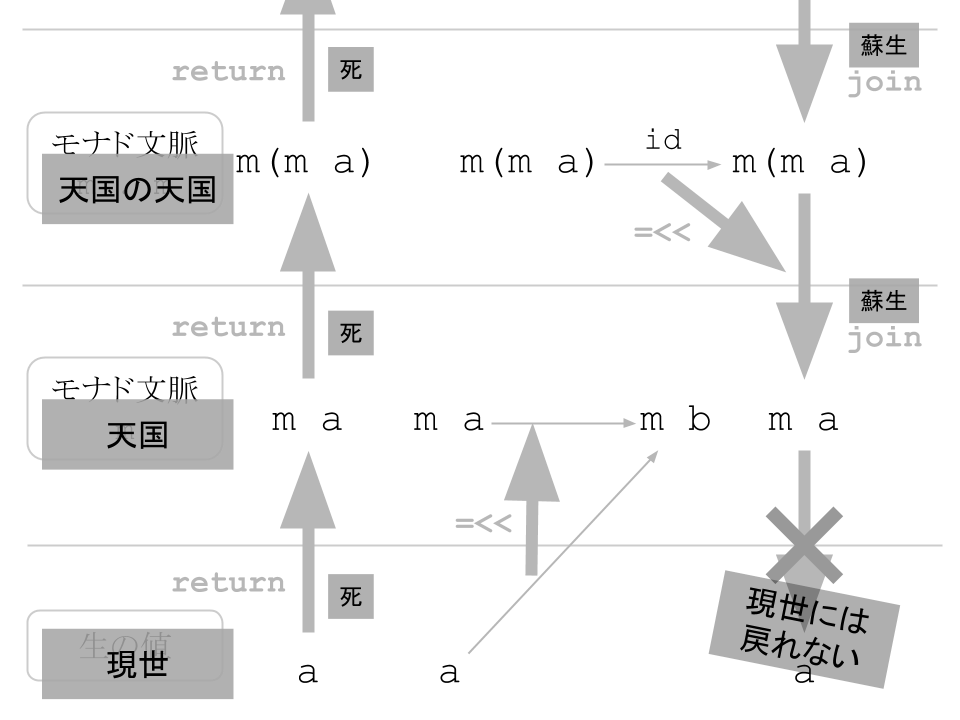
死をモナドの文脈とみなし, a を現世, m a をあの世の人であると仮定することで,以下のことを導きます.
return :: a -> m a が死ぬことに対応します.
m a -> a 型の)操作は用意されていません.つまり死んだら現世に生き返ることは出来ません.これは私たちも知っている事実ですね.
join :: m (m a) -> m a は,あの世のあの世からあの世に生き返ることに対応します.
return :: a -> m a と fmap :: (a -> b) -> (m a -> m b) と自然性条件によって天国でも通用することが担保されているので,現世の物理法則などもそのまま存在しているはずです.現世と似たような世界になっていると推測できます.
return :: a -> m a は a つまり人を何も変えずに文脈に入れる操作であり,通常は保たれます.つまり,知識をつけることはあらゆる世界において善いことです.
data Heaven a = H のように天国モナドが幽霊型である場合はその限りではありません.この例だと,全て生物は死後唯一の存在へと収束してしまいます.
return が意識をそのまま保って天国に移すものだとしても,身体的特徴は直接生死とは関係なく,保たれるかどうかはわかりません.また,もし保たれると仮定すると,寝たきりの老人が死んだら天国でも寝たきりということになり,少し残酷です.
return と名付けられているの?
return と =<< の概念と,自ずから導かれる join の概念,そして死をモナドの文脈に対応させること自体が教典であり,Q&Aも含めたその他の文書はモナド教における単なる解釈の一つです.
m が唯一ではないかもしれません.例えば死後の世界は天国と地獄の2つがあるという宗教もあります.先ほどのように幽霊型であるモナドかもしれません.果たしてどこに行くかは死んでみないとわかりませんし,一度そのモナドに入ったが最後,抜け出して別のモナドに入り直すことは永遠に出来ません.現世にいる限り,気軽に死なないほうが無難でしょう.天国に行ってからは思う存分にどうぞ.
return が自明な実装でない場合、人としての本質が変容する、つまり型が同じでも値は異なるという可能性がないですか?(質問)
f =<< (return x) == f x
return =<< m == m
join で生き返った人にも同様に,他の人になるのではないでしょうか。 id を用いるもの以外にも定義できる場合があるので。(質問)
id 以外の操作を =<< に渡した場合,確かに他の人や他の生物になる可能性はあります.ただ, id (私が私になるという自明の理)以外の操作の存在は確認していません.
m a -> a の存在を追い求める人たちは邪教になるのですか?(質問)
m (m a) -> m a であっただけのことで,依然としてモナド教の範疇です.
モナド教のサイトを公開しました https://t.co/3JBfJQ8cPs
— na2hiro@量子将棋の人 (@na2hiro) 2014, 8月 13